202503-1 荒地开垦
题目描述
小杨有一大片荒地,可以表示为一个 行 列的网格图。
小杨想要开垦这块荒地,但荒地中一些位置存在杂物,对于一块不存在杂物的荒地,该荒地可以开垦当且仅当其上下左右四个方向相邻的格子均不存在杂物。
小杨可以选择至多一个位置,清除该位置的杂物,移除杂物后该位置变为荒地。小杨想知道在清除至多一个位置的杂物的情况下,最多能够开垦多少块荒地。
输入格式
第一行包含两个正整数 ,含义如题面所示。
之后 行,每行包含一个长度为 且仅包含字符 . 和 # 的字符串。如果为 .,代表该位置为荒地;如果为 #,代表该位置为杂物。
输出格式
输出一个整数,代表在清除至多一个位置的杂物的情况下,最多能够开垦的荒地块数。
样例输入 1
3 5......#..#.....样例输出 1
11提示
【样例解释】
移除第二行从左数第二块空地的杂物后:
.........#.....第一行从左数前 块荒地,第二行从左数前 块荒地,第三行从左数前 块荒地,均可开垦,。
【数据范围】
对于全部数据,有 。
代码解析
今年第一次四级考题就使用了模拟法,没有什么技巧,认真读题暴力枚举即可,这里的偏移数组
dx[]和dy[]不是必要的,如果觉得思路受阻可以直接简单粗暴进行四个方向,对于代码的运行效率没有什么影响。
#include<bits/stdc++.h>using namespace std;int main() {
int n, m, max = 0; char a[1005][1005]; int dx[] = {0, 0, 1, -1}; int dy[] = {1, -1, 0, 0}; cin >> n >> m; for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) { cin >> a[i][j]; a[i][0] = a[i][m+1] = '.'; a[0][j] = a[n+1][j] = '.'; } int count = 0; for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++){ if (a[i][j] == '#') continue; bool flag = true; for (int k = 0; k < 4; k++) if (a[i+dx[k]][j+dy[k]] == '#') flag = false; if (flag) count++; } for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++){ int max_count = count; if (a[i][j] == '#') { bool flag = true; for (int k = 0; k < 4; k++) { int x = i+dx[k], y = j+dy[k]; if (a[x][y] == '#') {flag = false; break;} if (x >= 1 && x <= n && y >= 1 && y <= m) { int cnt = 0; for (int d = 0; d < 4; d++) if (a[x+dx[d]][y+dy[d]] == '#') cnt++; if (cnt == 1) max_count++; } } if (flag) max_count++; } max = (max_count > max ? max_count : max); } cout << max;
return 0;}202503-2 二阶矩阵
题目描述
小 A 有一个 行 列的矩阵 。
小 A 认为一个 的矩阵 是好的,当且仅当 。其中 表示矩阵 的第 行第 列的元素。
小 A 想知道 中有多少个好的子矩阵。
输入格式
第一行,两个正整数 。
接下来 行,每行 个整数 。
输出格式
一行,一个整数,表示 中好的子矩阵的数量。
样例输入 1
3 41 2 1 02 4 2 10 3 3 0样例输出 1
2提示
【样例解释】
样例中好的子矩阵如下:
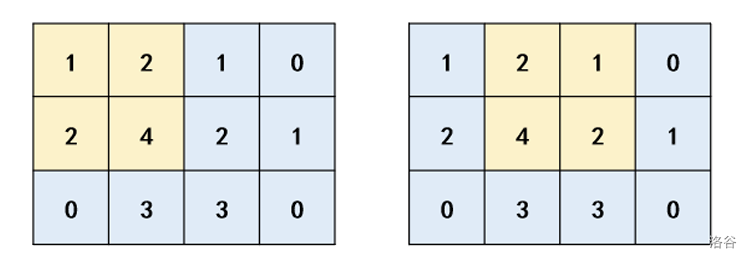
【数据范围】
对于所有测试点,保证 ,,
代码解析
枚举法啦,枚举就可以啦,没有啥难度嗷~ 注意细心一点,坐标之间的关系别搞混了。
#include<bits/stdc++.h>using namespace std;int main() {
int n, m, a[505][505], cnt = 0; cin >> n >> m; for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) cin >> a[i][j];
for (int i = 1; i <= n-1; i++) for (int j = 1; j <= m-1; j++) if (a[i][j] * a[i+1][j+1] == a[i][j+1] * a[i+1][j]) cnt++; cout << cnt;
return 0;}202506-1 画布裁剪
题目描述
小 A 在高为 宽为 的矩形画布上绘制了一幅画。由于画布边缘留白太多,小 A 想适当地裁剪画布,只保留画的主体。具体来说,画布可以视为 行 列的字符矩阵,其中的字符均为 ASCII 码位于 之间的可见字符,小 A 只保留画布中由第 行到第 行、第 列到第 列构成的子矩阵。
小 A 将画布交给了你,你能帮他完成画布的裁剪吗?
输入格式
第一行,两个正整数 ,分别表示画布的行数与列数。
第二行,四个正整数 ,表示保留的行列边界。
接下来 行,每行一个长度为 的字符串,表示画布内容。
输出格式
输出共 行,每行一个长度为 的字符串,表示裁剪后的画布。
样例输入 1
3 52 2 2 4......>_<......样例输出 1
>_<样例输入 2
5 51 2 3 4AbCdEfGhIkLmNoPqRsTuVwXyZ样例输出 2
CdhI提示
对于所有测试点,保证 ,,。
代码解析
这道题就是送分题,注意我们只需要输出题目要求输出的部分即可,不是真的需要将原数组裁剪。。。
#include<bits/stdc++.h>using namespace std;int main() {
char a[101][101]; int h, w, x1, x2, y1, y2; cin >> h >> w; cin >> x1 >> x2 >> y1 >> y2; for (int i = 1; i <= h; i++) for (int j = 1; j <= w; j++) cin >> a[i][j]; for (int i = x1; i <= x2; i++) { for (int j = y1; j <= y2; j++) cout << a[i][j]; cout << endl; }
return 0;}202506-2 排序
题目描述
体育课上有 名同学排成一队,从前往后数第 位同学的身高为 ,体重为 。目前排成的队伍看起来参差不齐,老师希望同学们能按照身高从高到低的顺序排队,如果身高相同则按照体重从重到轻排序。在调整队伍时,每次只能交换相邻两位同学的位置。老师想知道,最少需要多少次交换操作,才能将队伍调整成目标顺序。
输入格式
第一行,一个正整数 ,表示队伍人数。
接下来 行,每行两个正整数 和 ,分别表示第 位同学的身高和体重。
输出格式
输出一行,一个整数,表示最少需要的交换次数。
样例输入 1
51 603 702 804 554 50样例输出 1
8样例输入 2
54 04 02 03 01 0样例输出 2
1提示
对于所有测试点,保证 ,。
代码解析
这道题考察的是结构体数组的冒泡排序,注意排序中交换的条件有两条,一个是只看身高,另一个是身高相同的时候看体重,这是为数不多的考集中直接考察排序的题目,说明排序在编程题中考察的概率还是有的。
#include<bits/stdc++.h>using namespace std;struct student { int h, w;}a[3005];int main() {
int n, cnt = 0; cin >> n; for (int i = 1; i <= n; i++) cin >> a[i].h >> a[i].w; // 冒泡排序 for (int i = 1; i <= n-1; i++) for (int j = 1; j <= n-i; j++) if (a[j].h < a[j+1].h || a[j].h == a[j+1].h && a[j].w < a[j+1].w) { swap(a[j], a[j+1]); cnt++; } cout << cnt;
return 0;}202509-1 排兵布阵
题目描述
作为将军,你自然需要合理地排兵布阵。地图可以视为 行 列的网格,适合排兵的网格以 1 标注,不适合排兵的网格以 0 标注。现在你需要在地图上选择一个矩形区域排兵,这个矩形区域内不能包含不适合排兵的网格。请问可选择的矩形区域最多能包含多少网格?
输入格式
第一行,两个正整数 ,分别表示地图网格的行数与列数。
接下来 行,每行 个整数 ,表示各行中的网格是否适合排兵。
输出格式
一行,一个整数,表示适合排兵的矩形区域包含的最大网格数。
样例输入 1
4 30 1 11 0 10 1 11 1 1样例输出 1
4样例输入 2
3 51 0 1 0 10 1 0 1 00 1 1 1 0样例输出 2
3提示
对于所有测试点,保证 ,。
代码解析
没有技巧,根据题意使用模拟法解题即可,简而言之,可选择的矩形区域必须全都是 1,只需要以每个点
arr[i][j]作为起点,再以这个点为矩形左上角,依次枚举右下角的点arr[x][y],遍历这个矩形区域,看这个区域内是否全部都是 1,如果全部都是 1 则统计这个矩形区域内点的数量(x-i+1)*(y-j+1),求最大值。
#include<bits/stdc++.h>using namespace std;bool arr[15][15] = {0};int n, m;
// 封装 sum 函数统计以 arr[i][j] 作为左上角的矩形中全是 1 的最大矩形int sum(int i, int j) { int cnt = 0; for(int x = i; x <= n; x++) for(int y = j; y <= m; y++) { bool flag = true; for(int a = i; a <= x; a++) for(int b = j; b <= y; b++) if (arr[a][b] == 0) flag = false; if (flag) cnt = max(cnt, (x-i+1)*(y-j+1)); } return cnt;}
int main() {
cin >> n >> m; int ans = 0; for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++) cin >> arr[i][j]; for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++) { ans = max(ans, sum(i, j)); } cout << ans;
return 0;}202509-2 最长连续段
题目描述
对于 个整数构成的数组 ,如果对 都有 ,那么称数组 是一个连续段。
给定由 个整数构成的数组 ,你可以任意重排数组 中元素顺序。请问在重排顺序之后, 所有是连续段的子数组中,最长的子数组长度是多少?
例如,对于数组 ,可以将其重排为 ,有以下 个子数组:
其中除 以外的子数组均是连续段,因此是连续段的子数组中,最长子数组长度为 3。
输入格式
第一行,一个正整数 ,表示数组长度。
第二行, 个整数 ,表示数组中的整数。
输出格式
一行,一个整数,表示数组 重排顺序后,所有是连续段的子数组的最长长度。
样例输入 1
41 0 2 4样例输出 1
3样例输入 2
99 9 8 2 4 4 3 5 3样例输出 2
4提示
对于 的测试点,保证 。
对于所有测试点,保证 ,。
代码解析
连续段的意思是 1,2,3,4 …
解题思路就是先对原数组进行排序,然后确定一个变量
last来记录上一个数字,如果数a[i] == last,就跳过继续找,如果a[i] == last + 1则连续段长度加 1,如果a[i]小于last或大于last + 1说明当前连续段已经最长,记录最大值,重新开始统计下一个连续段
#include<bits/stdc++.h>using namespace std;int main() {
int a[100005]; int n; cin >> n; for(int i = 0; i < n; i++) cin >> a[i]; sort(a, a+n); int last = a[0], m = 1, cnt = 1; for(int i = 1; i < n; i++) { if (a[i] == last) { continue; } else if (a[i] == last + 1) { m++; last = a[i]; } else { cnt = max(cnt, m); m = 1; last = a[i]; } } cnt = max(cnt, m); cout << cnt;
return 0;}202512-1 建造
题目描述
小 A 有一张 行 列的地形图,其中第 行第 列的数字 代表坐标 的海拔高度。
停机坪为一个 的区域,且内部所有 个点的最大高度和最小高度之差不超过 。
小 A 想请你计算出,在所有适合建造停机坪的区域中,区域内部 个点海拔之和最大是多少。
输入格式
第一行三个正整数 ,含义如题面所示。
之后 行,第 行包含 个整数 ,代表坐标 的高度。
数据保证总存在一个适合建造停机坪的区域。
输出格式
输出一行,代表最大的海拔之和。
样例输入 1
5 5 35 5 5 5 55 1 5 1 55 5 5 5 55 2 5 2 53 5 5 5 2样例输出 1
40提示
数据范围
对于所有测试点,保证 ,。
代码解析
这道题重点考的还是二维数组来枚举解题,因为数据范围较小,这道题直接暴力解题即可,根据题意我们枚举出来每个 的区域左上角坐标 ,然后遍历这块区域找出最大值最小值以及计算累加和,判断是否符合条件,符合条件就更新答案。
#include <iostream>using namespace std;int main() {
int m, n, h, ans = 0, mp[1005][1005]; cin >> m >> n >> h; for(int i = 1; i <= m; i++) for(int j = 1; j <= n; j++) cin >> mp[i][j]; for(int i = 1; i <= m-2; i++) for(int j = 1; j <= n-2; j++) { int mx = -1, mi = 100005, sum = 0; for (int x = i; x <= i+2; x++) for (int y = j; y <= j+2; y++) { sum += mp[x][y]; mx = max(mx, mp[x][y]); mi = min(mi, mp[x][y]); } if (mx-mi <= h) ans = max(ans, sum); } cout << ans;
return 0;}202512-2 优先购买
题目描述
小 A 有 元预算。商店有 个商品,每个商品有商品名 、价格 和优先级 三种属性,其中 为正整数,且 越小代表商品的优先级越高。
小 A 的购物策略为:
- 总是优先买优先级最高的东西;
- 如果有多个最高优先级商品,购买价格最低的;
- 如果有多个优先级最高且价格最低的商品,购买商品名字典序最小的。
小 A 想知道能购买哪些商品。
输入格式
第一行两个正整数 ,代表预算和商品数。
之后 行,每行一个商品,依次为 ,代表第 个商品的商品名、价格、优先级。
数据保证不存在两个名字相同的商品。
输出格式
按照字典序从小到大的顺序,输出所有购买商品的商品名。
样例输入 1
20 4apple 6 8bus 15 1cab 1 10water 4 8样例输出 1
buscabwater提示
数据范围
对于所有测试点,保证 ,,,。商品名仅由小写字母组成且不存在两个相同的商品名。
代码解析
这道题主要考察的是结构体排序,先按照题目要求排序,然后筛选出来符合预算的商品,最后再次按照筛选出来的物品的字典序排序输即可,这里筛选出来的物品可以使用字符串数组,这样后续排序比较简单。
#include <bits/stdc++.h>using namespace std;struct stu { string s; int p, v;};bool cmp(stu a, stu b) { if (a.v != b.v) return a.v < b.v; else if (a.p != b.p) return a.p < b.p; else return a.s < b.s;}int main() {
int m, n; cin >> m >> n; stu a[1005]; string s[1005]; for (int i = 0; i < n; i++) cin >> a[i].s >> a[i].p >> a[i].v; sort(a, a+n, cmp); int cnt = 0; for (int i = 0; i < n; i++) { if (m < a[i].p) continue; s[cnt++] = a[i].s; m -= a[i].p; } sort(s, s+cnt); for (int i = 0; i < cnt; i++) cout << s[i] << endl;
return 0;} 陕公网安备61010302001363号
陕公网安备61010302001363号